三位数乘两位数_三位数乘两位数速算技巧

1.三位数乘两位数的列竖式计算

2.三位数乘两位数怎么验算呢？

3.3位数乘2位数的算式是什么?

用1、2、3、4、5组成一个三位数乘两位数。乘积最大应该是：431×52=22412，乘积最小应该是：13×245=3185。

乘积最大和最小的规律：

将若干个数字组成几个多位数相乘，使得它们的乘积最大或最小，是有一定的规律可循的，下面一用四个数字组成两个两位数的问题为例；

仔细进行分析：用1、2、4、6四个数字组成两个两位数，要使组成的两个两位数的乘积最大，组成的这两个数的十位上的数字应该是6和4。因此，组成的两个两位数就有两种可能：(1)62×41；(2)61×42。经过计算发现：61×42＞62×41。

观察上面的两个竖式：这两个算式的十位上的两个数字相乘的积是相同的，个位上的两个数字相乘的积也是相同的(红色的数字)，都是6×4＝24个百和 1×2＝2个一；

但是十位上的数字分别与个位上的数字相乘的积却是不同的(蓝色的数字)，左边一个竖式是6个十和8个十的和，右边一个竖式是12个十和4 个十的和，这样在十位上是第二个算式的和比较大，这样，最终就是第二个算式的积大。

经过观察、比较，可以得出，要使组成的两个数乘积最大，这两个数必须符合下面两点，大数尽可能排在高位，两个两位数的差尽可能小。

扩展资料

整数数位顺序表：“数级：亿级、万级、个级。

数位：千亿位、百亿位、十亿位 、亿位、千万位、百万位、十万位、万位、千位、百位、十位。

不同计数单位，按照一定顺序排列，它们所占位置叫做数位。在整数中的数位是从右往左，逐渐变大；第一位是个位，第二位是十位，第三位是百位，第四位是千位，以此类推。同一个数字，由于所在数位不同，计数单位不同，所表示数值也就不同。

整数的乘法：

(1)从个位乘起，依次用第二个因数每位上的数去乘第一个因数；

(2)用第二个因数那一位上的数去乘，得数的末位就和第二个因数的那一位对齐；

(3)再把几次乘得的数加起来。

三位数乘两位数的列竖式计算

三位数乘两位数算法：

1、三位数与两位数的个位和个位要对齐，十位数要跟十位数对齐。

2、先用两位数的个位分别与三位数的每一位数相乘。

3、再用两位数的十位分别与三位数的每一位数相乘，乘得结果的个位要与前面结果的十位对齐。

4、然后两个结果相加就得到三位数乘两位数的结果了。

扩展资料：

计算“三位数乘两位数”要做到：

乘的次序要正确：先用两位数的个位去乘三位数，得到有多少个一，再用两位数的十位去乘三位数，得到有多少个十。

注意：乘数的哪一位去乘被乘数，得数的末位就要和哪一位对齐。最后把两次乘得的积相加。

三位数乘两位数怎么验算呢？

三位数乘两位数例子解析812×451

解题思路:先将两乘数末位对齐,然后分别使用第二个乘数,由末位起对每一位数依次乘上一个乘数,最后将所计算结果累加即为乘积,如果乘数为小数可先将其扩大相应的倍数,最后乘积在缩小相应的倍数；

解题过程:

步骤一:1×812=812

步骤二:5×812=40600

步骤三:4×812=324800

根据以上计算结果相加为366212

验算:366212÷451=812

扩展资料(验算结果):将被除数从高位起的每一位数进行除数运算,每次计算得到的商保留,余数加下一位数进行运算,依此顺序将被除数所以位数运算完毕,得到的商按顺序组合,余数为最后一次运算结果

解题过程:

步骤一:3662÷451=8 余数为:54

步骤二:541÷451=1 余数为:90

步骤三:902÷451=2 余数为:0

根据以上计算步骤组合结果为812

存疑请追问,满意请纳

3位数乘2位数的算式是什么?

三位数乘两位数的验算方法：除法。用两个因数的积除以一个因数，如果得到另一个因数则运算正确。

举例说明如下：

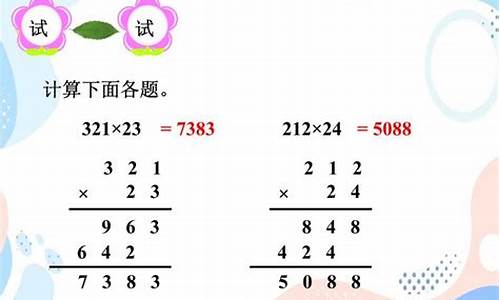
三位数321乘以两位数21，数学表达式：321×21=3741。竖式如下：

验算即为除法：用两个因数的积除以一个因数，如：6741÷21=321。竖式如下：

扩展资料：

整数的除法法则

1）从被除数的高位起，先看除数有几位，再用除数试除被除数的前几位，如果它比除数小，再试除多一位数；

2）除到被除数的哪一位，就在那一位上面写上商；

3）每次除后余下的数必须比除数小。

除法竖式计算方法有个歌谣：

除数一位看一位，?一位不够看两位。?除到哪位商哪位，?哪位不够零占位。?每次除后要比较，?余数要比除数小。

1、从被除数的高位除起，先用除数试除被除数的前两位数，如果比除数小，再试除前三位数。

2、除到被除数的哪一位，就在那一位上面写商。

3、求出每一位商，余下的数必须比除数小。

计算如下：102×25=2550。

乘法运算

1、同号得正，异号得负，并把绝对值相乘。

2、任何数与零相乘，都得零。

3、几个不等于零的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负，当负因数有偶数个时，积为正。

4、几个数相乘，有一个因数为零，积就为零。

5、几个不等于零的数相乘，首先确定积的符号，然后后把绝对值相乘。